Abstracts Mathematical Ability Conference

Moving Perception Forward in Learning Sciences Discourse

Dor Abrahamson, University of California, Berkeley

Among educational researchers inspired by the embodied turn in the cognitive sciences, there is much ado about doing. Students’ motor behavior (the dynamic temporal–spatial kinesiological process of “doing”), historically eclipsed by its situated outcomes (the static, material, logical product of “done”), is now in the limelight of methods (innovative instruments generating movement data for multimodal learning analytics) and theorization (coordination-dynamics models of shifts between dynamical equilibria). By this token, while perception may be critical for enacting movement, it plays no more than a supporting role. This theoretical view is liable to engender a kinesiological emphasis in educational practice, where motor techniques are taught directly as a didactical means of improving student performance on manipulation tasks. Drawing on kinesiology (Bernstein, 1996), ecological psychology (Gibson, 1966; Heft, 1989; Turvey, 2019), Gestalt theory of motor control (Mechsner, 2003; Mechsner, Kerzel, Knoblich, & Prinz, 2001), enactivist theory (Hutto, Kirchhoff, & Abrahamson, 2015; Varela, Thompson, & Rosch, 1991), and dance philosophy (Sheets-Johnstone, 1981, 2015, 2018), I interrogate the putative prominence of motor coordination in the phenomenology of enacting movement. Rather, I put forth, improvement to motor performance is epiphenomenal and consequential to the perceptual discovery of affordances in the situated domain of enactment. Once we discover how we should move to get a task done, motor actions self-assemble to enact that movement. As such, learning to move in new ways may take practice, but one’s attention and reflection are essentially on movement forms and feedback sensation, not on the intricacies of kinesiological selections, control, and performance. I offer implications for the design, facilitation, and evaluation of instructional activities, where students learn to enact movement forms that instantiate presymbolic mathematical notions. The good news is that shifting the heft of our field’s discourse from motor action to sensorimotor perception untethers the theorized phenomenology of embodied learning from the corporeal specification of particular situated enactments, opening its horizons to vistas of cross-situational application.

Bernstein, N. A. (1996). Dexterity and its development. In M. L. Latash & M. T. Turvey (Eds.), (pp. 3-235). Mahwah, NJ: Lawrence Erlbaum Associates.

Gibson, J. J. (1966). The senses considered as perceptual systems. Boston: Houghton Mifflin.

Heft, H. (1989). Affordances and the body: An intentional analysis of Gibson’s ecological approach to visual perception. Journal for the Theory of Social Behaviour, 19(1), 1–30.

Hutto, D. D., Kirchhoff, M. D., & Abrahamson, D. (2015). The enactive roots of STEM: Rethinking educational design in mathematics. In P. Chandler & A. Tricot (Eds.), Human movement, physical and mental health, and learning [Special issue]. Educational Psychology Review, 27(3), 371-389.

Mechsner, F. (2003). Gestalt factors in human movement coordination. Gestalt Theory, 25(4), 225-245.

Mechsner, F., Kerzel, D., Knoblich, G., & Prinz, W. (2001). Perceptual basis of bimanual coordination. Nature, 41(6859), 69-73.

Sheets-Johnstone, M. (1981). Thinking in movement. Journal of Aesthetics and Art Criticism, 39(4), 339-407.

Sheets-Johnstone, M. (2015). Embodiment on trial: A phenomenological investigation. Continental Philosophy Review, 48(1), 23-39. Retrieved from http://dx.doi.org/10.1007/s11007-014-9315-z. doi:10.1007/s11007-014-9315-z

Sheets-Johnstone, M. (2018). Why kinesthesia, tactility and affectivity matter: Critical and constructive perspectives. Body & Society, 24(4), 3-31. Retrieved from https://journals.sagepub.com/doi/abs/10.1177/1357034X18780982. doi:10.1177/1357034×18780982

Turvey, M. T. (2019). Lectures on perception: An ecological perspective. New York: Routledge / Taylor & Francis.

Varela, F. J., Thompson, E., & Rosch, E. (1991). The embodied mind: Cognitive science and human experience. Cambridge, MA: M.I.T. Press.

Realist but speculative: Metamorphic concepts and mathematical response-ability

Liz de Freitas, Manchester Metropolitan University

This presentation takes up the question of mathematical ability as part of an agential realist and new materialist philosophy of mathematics. The work is situated in philosophies of immanence (non-dualist) for which the matter-concept mixture entails a flat ontology. My focus is on how mathematical ability is a kind of environ/mentality, and thus ‘belongs’ to a more-than-human metamorphic ecology. I aim to show that such grand speculative claims can help us make sense of everyday humble mathematical endeavours in terms of affective material practices, directing our attention to the transindividual response-ability for learning and achievement.

Pregnant Moments in the Course of Things

Alfred Nordmann, Technische Universität Darmstadt

The title of this talk refers to artworks and a machine-like unfolding
of events. These involve notions of implication or consequence. Rather
than seek to clarify, analytically, how these notions are related to
their mathematical counterparts, I will focus on achievements of
technical control in the sphere of the physical as well as symbolic
composition of things. If mathematical reasoning requires the ability to
exhibit relations among symbols, how is that different, if at all, from
the ability to arrange machine elements to form a structure which
behaves predictably? And what, then, is the relation between
demonstration by showing and by experiment? Answers to such  questions
have been suggested by Wittgenstein.

Some Perspectives on Mathematical Ability

Valentin Goranko, Stockholm University

I will discuss several perspectives on mathematical ability — philosophical, mathematical, computational, and formal logical perspective — relating it to knowledge, reasoning resources and skills, and algorithmic realisability. I will then propose and discuss some logical formalisations purporting to reflect the concept of ability in general, and mathematical ability in particular.

The roots of mathematical abilities

Karim Zahidi, University of Antwerp

Popular theories in the area of mathematical cognition hold that we possess some mathematical abilities “by nature”. In particular, some elementary numerical and geometrical abilities are considered to be part of our biological endowment and serve as a stepping stone for the development of more advanced mathematical abilities. As a consequence both the ontogenetic and socio-genetic development of mathematical abilities are, according to these theories,  rooted in biologically constituted mathematical abilities. In this talk I will argue that these theories fail to explain the origins of mathematical cognition both on a ontogenetic and socio-genetic level. One of the reasons that they fail to meet their explanatory target , or so I will argue, is that they start from a problematic view of what cognition amounts to. According to that view cognition is always a matter of manipulating mental representations. I will show that applying this view to mathematical cognition leads to circular explanations. Abandoning the idea of cognition as representation manipulation, leads to a different, and less problematic, view of mathematical cognition. Drawing on insights from the enactive approach to cognition, I will sketch such an alternative view of the socio-genetic development of mathematical cognition.  In particular, I will show that starting from non-mathematical cognitive capacities it is only through socially mediated material practices that mathematical abilities arise.  My focus will be mainly on numerical cognition, but I will  conclude with some remarks on how this framework might be extended to incorporate other mathematical abilities.

Mathematics cognition and the return of the body

Luis Radford, Laurentian University

Current discussions on the role of the body in our acts of knowing have provoked both enthusiasm and skepticism. Redefining the epistemological role of the body has led, indeed, to new approaches to the old problem of knowledge—what is to be known and how it is to be known. For some scholars, like Terry Eagleton, however, the current enchantment with embodiment is in the end no more than “the return in a more sophisticated register of the old organicism” or else a token of “the post-modern cult of pleasure” and love for the concrete (Eagleton, 1998). In this talk, I argue that an account of the embodied nature of mathematical cognition must come to terms with the problem of the relationship between the body as a locus for the constitution of an individual’s subjective meanings and the cultural (material and ideational) world that bodies touch, perceive, feel, and sense. I explore here an idea according to which sentient bodies and sensed objects constitute each other in concrete cultural-historical activity; that is, in praxis.

Rhythm and Ordinal Counting

Ricardo Nemirovsky, Manchester Metropolitan University

“Counting is so important in music!” said Andy, a friend and musician.  This remark from a couple of years ago triggered the pursuit of inquiries that led to the present paper.  Why would counting be significant in musical performance?  Given that the counting at stake usually goes up to four or eight at a regular pace, it seems a rather trivial matter for any competent counter.  What could it add to the copiously complex range of issues involved in the production of music?  Since then we have worked with children and teenagers learning to drum, individually or in groups, through sequences of sessions taught by Andy.  It became apparent to us that the key outcome of counting in this context is not so much numerosity; such as the number of times a drum is to be stricken during a measure, but rhythm.  This prompted us to reflect less on cardinal counting that is focused on ascertaining numerosity, and more on ordinal counting.  This paper examines numbers as events and counting as a dynamic genesis of complex and bodily events.

On the (In)dispensability of Action Types

Alexandra Kuncová, Utrecht University

In my talk, I explore the analysis of ability. Imagine that we flip a coin out of your sight and ask you to bet how it lands – heads or tails. Are you able to win the bet? In a certain sense, yes — we refer to this as causal ability. There are two actions available to you and one of them guarantees that you bet correctly. However, in the epistemic sense, you are not able to win the bet, because you do not know which of those two actions actually guarantees the result.

In my presentation I elaborate on epistemic ability and two ways of modelling it. The standard analysis relies on action types — as opposed to action tokens — and states that an agent has the epistemic ability to do something if and only if there is an action type available to her that she knows guarantees it. I will show, however, that these action types are dispensable: I will present a formalism without action types that can simulate the standard analyses of epistemic ability that rely on action types.

In light of this dispensability of action types in an epistemic setting I will finish by reflecting on whether action types might be useful for other senses of agency and ability.

(This is based on joint work with Jan Broersen, Hein Duijf, and Aldo Ramirez Abarca.)

“What is it to do mathematics?” Reflections from an analysis of Children’s mathematics

Jérôme Proulx, UQAM

In mathematics education research, we often attempt to understand people’s (be them pupils, adult solvers, teachers, etc.) ways of making sense of mathematics. We mostly do this, implicitly or at times explicitly, through comparing what they do to with the established mathematical concepts and methods (actual, as well as historical ones), taken as referents. This approach has led to many significant insights on how students understand and do mathematics (and how we can think of ways of helping them do and understand mathematics). However, the research we conduct on mental mathematics in various classrooms led us to begin being interested in turning this issue upside-down, that is, to begin considering using students’ ways of doing mathematics to study what mathematics is and what it means to do mathematics. Said differently, students doing mathematics while solving mental mathematics tasks made us reflect on what (doing) mathematics implies and what mathematical activity is all about. This orientation led us to directly address the question at the core of the conference call, mainly “What is it to do mathematics?”. In this paper, analyses of solvers’ mental mathematics strategies on a variety of mathematical topics will be scrutinized to bring forth the ways in which mathematical activity is enacted and what it means to do mathematics in this context. In particular, mental mathematics strategies, conceived as emergent events, will be discussed as (1) enacted in action, (2) situated, and (3) deployed in-the-moment by solvers in relation to prompts given to them. These dimensions, drawn out from studies on mental mathematics, will be used in return to shed light and advance on the question “What is it to do mathematics?” from a more general point of view.

Mathematics as/is an activity: from ability to enacting

Jean-François Maheux & Jérôme Proulx, UQAM

When students engage in solving mental mathematics questions (in arithmetic, algebra, geometry, and so on), they offer solutions that are often surprising. Although it is possible to pinpoint concepts and methods in their solution paths, or strategies, that are part of the regular school curriculum (e.g., fractions, arithmetic mean, dividing, isolating x), the ways they engage with tasks are seldom explicitly taught to them. One main reason for this is the very local nature of the approaches they engage with. For example, some solutions hinge on the particular numbers present in an equation, or the specific position of a point on the plane, and others involve mathematically problematic moves that turn out to produce valid answers in the case at hand. Whereas one might ask how and where these solutions originate (e.g., which concepts are creatively used or combined, how and why), we rather became interested in analyzing solutions in terms of mathematical activities in themselves, as emergent mathematical events. This venture toward emergence forced us to move away from a cognitive/psychological subject that possess knowledge, and toward an experiential/phenomenological subject that (en)acts. Committing to this perspective raises issues in regard with what exactly would be a mathematical ability. Reviewing the questions guiding the conference call, one might indeed notice how some formulations could be seen as assuming that a mathematical ability is something we can acquire, something we have; the term “ability” might in itself be suggestive of this, implying a “capacity” to act. In this paper, we propose to examine the mathematical ideas brought forth by some students’ ways of solving, in mental mathematics contexts, through Varela’s (1999) conceptualization of know-how: a readiness-for-action, a disposition, a form of embodied action we enact. We thus explain how this framing of the question of mathematical ability is coherent with our conceptualization of mathematical activity as Doing|mathematics, which is based on the observation that doing mathematics is both doing something recognizable as mathematics, and what we do when we say we do mathematics.

Varela, F. J. (1999). Ethical know-how. Stanford, US: Standford University Press.

Integrating the hand into mathematics: folding and braiding as a case study

Michael Friedman, Humboldt University

How did one consider material, tactile or haptic mathematical activities during the 20th century in the mathematical research community? These activities – such as construction of models from various materials, folding polygons or polyhedra, or knotting strings – were (any sometime still are) considered either as a childish play or, at best, as only bringing to our senses the abstract mathematical objects which one already discovered. However, a closer look at the history of mathematics shows that during the 19th century the physical construction of models – for example, of curves and surfaces, either from wood, plaster or strings – was considered also as an epistemic activity, i.e. as what prompts the emergence of new mathematical knowledge (Brill 1887). Taking a clue from this tradition, one may ask whether the mathematization during the 20th century of material, manual practices – such as folding and braiding (see: Row 1893, Beloch 1934, and Artin 1926; see also: Friedman 2018) – not only considered them as epistemic but also took into account this manual activity even after these practices were formualized, i.e. presented with the help of mathematical symbols.

In my talk I would like to suggest an affirmative answer. Based on two historical case studies (the mathematization of folding and braiding), I claim that the manual activity was an essential part how mathematical knowledge was transmitted and embodied. This indeed stands in line with the latest research of (Eddy 2018), claiming that that in the 18th and 19th centuries, material “adaptable folding, writing, and drawing techniques” were used to teach mathematics in schools; the hand itself was embedded into acquiring mathematical knowledge. Hence, not only that the folding or the braiding hand was essential, but also the manual, material action itself was carrying with it a reasoning, which could not be reduced to a syntactic–symbolical one.

Bibliography:

Artin, Emil (1926), “Theorie der Zöpfe”, Abh. math. Sem. Hamburg 4, p. 47-72.

Beloch, Margherita Beloch (1934), “Alcune applicazioni del metodo del ripiegamento della carta di Sundara-Row.” Atti dell’Acc. di Scienze, Mediche. Nat Mat Ferrara Serie II 11, p. 186–189.

Brill, Alexander (1887), “Über die Modellsammlung des mathematischen Seminars der Universität Tübingen (Vortrag vom 7. November 1886)”, Math Naturwiss Mitt. 2, p. 69–80.

Eddy, Matthew Daniel (2018), “The Nature of Notebooks: How Enlightenment Schoolchildren Transformed the Tabula Rasa”, Journal of British Studies 57, p. 275–307.

Friedman, Michael (2018), A History of Folding in Mathematics. Mathematizing the Margins, Basel: Birkhäuser.

Row, Sundara Tandalam (1893), Geometrical exercises in paper folding. Addison, Madras.

Knowing When: The Circle

Eva Knoll, Mount Saint Vincent University

Knowing mathematics, as an active undertaking, is sometimes seen as involving three components: knowing that (e.g. number facts), knowing how (e.g. algorithms) and knowing why (understanding). At MathWeave we investigate the relationship between doing mathematics, making art (and craft), and education. As part of this work, we have been reflecting, debating, reading and writing about mathematical activity, knowing and understanding. This work has led us to consider a fourth kind of knowing, often overlooked in the pursuit of mathematical competency: ‘knowing when’. We propose to develop this additional element, and illustrate it using the circle. Throughout schooling, the circle is taught for its own sake as well as used as the foundation for other topics, in many topical contexts, including: basic geometry (naming and comparing forms), fractions (representing part‐whole relationships), data management (pie‐charts), trigonometry (the unit circle), topology (an example of a simple closed curve). Depending on the specific topic, different properties of the circle—even different conceptions of the circle—are used. Even a learner who has a grasp all of these conceptions, it is still necessary to develop a sense for which conception is the relevant one in each specific case.

A contextual approach to explanatory proofs

Joachim Frans, Vrije Universiteit Brussel

About 30 years ago, Mark Steiner (1978) started a small but still continuing line of research in the philosophy of mathematics, a line of research that focuses on the distinction between explanatory and non-explanatory proofs in mathematics. The underlying idea behind this is that all proofs show that a theorem is true, but some proofs do more and show why a theorem is true. Several philosophers have argued that it is possible to make an objective distinction between explanatory and non-explanatory proofs, while others argue this distinction is meaningless or purely subjective at best.

I will present a new perspective where the proof is not looked at in a vacuum, but at what role the proof potentially plays in the understanding-seeking activities of constructing and evaluating explanations. The result is that one cannot identify a proof as an explanation by only looking at the features of the proof. We speak of an explanatory proof if, in a specific context, the proof plays a crucial role in attaining better understanding of the theorem. This requires an appropriate match between the features of a proof, the knowledge/skill corpus of an agent and the epistemic aims of an agent. Following Jeremy Avigad (2008), who provides a rare attempt to provide an explicit account of understanding in philosophy of mathematics, I define understanding in terms of the possession of abilities.

I will argue that this new contextual perspective helps to overcome certain deadlocks in the debate, and drives us towards new philosophical questions that are currently largely ignored. More specifically, it stresses the importance of investigating mathematical abilities in order to have a nuanced and informed discussion about the relation between mathematical explanation and understanding.

Avigad, J. (2008), Understanding proofs, in P. Mancosu, ed., ‘The philosophy of mathematical practice’, Oxford University Press, pp. 317–353.

Steiner, M. (1978), ‘Mathematical explanation’, Philosophical Studies 34(2), 135 – 151.

Students construct and reconstruct geometrical knowledge using their body: Tal and Sean explore the mutual placement of straight lines and planes in geometrical space

Anatoli Kouropatov, Levinsky College of Education

Fischbein (1993) argued that geometry deals with mental entities which possess a character that is simultaneously conceptual and figural – so-called figural concepts. Fischbein claimed that “the main task of mathematics education (in the domain of geometry) is to create types of didactical situations which would systematically ask for a strict cooperation between the two aspects, up to their fusion in unitary mental objects” (ibid., p.161). Working with students from different populations (regular high school students, advanced high school students, and first and second year engineering students), we observed quite a strong pattern of student behavior: all students confronted a geometry task about the mutual placement of straight lines and planes in geometrical space using (only) their own bodies, as well as some concrete accessories. We argue that students’ body movements (with or without concrete accessories) become cognitive artifacts (in the Vigotskian perspective) used by learners as tools of semiotic mediation (Bartolini Bussi, & Mariotti, 2008) in their cognition–action interactions. Researchers that studied embodied cognition claim that mathematical reasoning draws on the coordination of motor and language systems (Abrahamson & Trninic, 2015; Alibali & Nathan, 2012). We conjecture that in the case of figural concepts, cognition–action interactions work mainly backwards (in terms of the GEMC theory hypothesis (Nathan, 2017)); actions induce cognitive states through a process of action–cognition transduction. In the conference we will demonstrate the empirical evidence of students’ knowledge construction, and we will discuss the possible meanings of our conjecture and its didactical implications.

Abrahamson, D., & Trninic, D. (2015). Bringing forth mathematical concepts. ZDM – International Journal on Mathematics Education, 47(2), 295-306.

Alibali, M. W., & Nathan, M. J. (2012). Embodiment in mathematics teaching and learning. Journal of Learning Sciences, 21(2), 247-286.

Bartolini Bussi, M. G., & Mariotti, M. A. (2008). Semiotic mediation in the mathematics classroom: Artifacts and signs after a Vygotskian perspective. In L. English, M. Bartolini Bussi, G. Jones, R. Lesh, & D. Tirosh (Eds.), Handbook of International Research in Mathematics Education (2nd ed.) (pp. 746–783). Mahwah, NJ: Lawrence Erlbaum.

Fischbein, F. (1993). The Theory of Figural Concepts. Educational Studies in Mathematics, 24(2), 139-162.

Nathan, M. J. (2017). One function of gesture is to make new ideas. In R. B. Church, M. W. Alibali, & S. D. Kelly, (Eds.) Why gesture? How the hands function in speaking, thinking, and communicating. Amsterdam: John Benjamins.

Mathematics from a linguistic perspective

Jos Tellings, Utrecht University

Linguistics studies the human capacity for language. Mathematics does not study the human capacity to do mathematics, but rather puts it into action. This makes mathematics unique within the sciences, and creates a ‘diagonal’ relationship between mathematics on the one hand and cognitive sciences such as linguistics on the other.

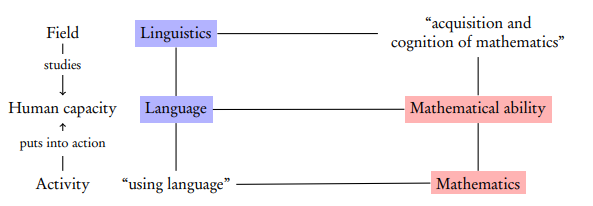
In this talk I show how taking a linguistic perspective affords a novel view on this special position of mathematical science.

I start by briefly reviewing some well-known connections between linguistics and mathematics, including methodological ones ( the use of mathematics in formal syntax and semantics), and historical ones ( the origin of modern linguistics from early 20th century developments in mathematics). However, I will mostly focus on cognitive links, in particular the acquisition of linguistic and mathematical abilities.

First language acquisition is a process that is fast, uniform, and does not require explicit training. Many (advanced) mathematical abilities, on the other hand, are not acquired uniformly and require explicit training. I will discuss work on the relation between number word learning and the grammatical marking of number (Almoammer et al. 2013; Marušič et al. 2016), and how the linguistic encoding of concepts such as number and scales plays a role in mathematical abilities. I will also discuss work on the role of mathematical abilities in the acquisition and interpretation of quantified phrases, which requires estimating and comparing the cardinalities of sets (Barner et al. 2009, Lidz et al. 2011).

Almoammer, A., Sullivan, J., Donlan, C., Marušič, F., Žaucer, R., O’Donnell, T.,& Barner, D. (2013). Grammatical morphology as a source of early number word meanings. Proc Natl Acad Sci USA.

Barner, D., Chow, K., & Yang, S. J. (2009). Finding one’s meaning: A test of the relation between quantifiers and integers in language development. Cognitive psychology, 58(2), 195–219.

Lidz, J., Pietroski, P., Halberda, J., & Hunter, T. (2011). Interface transparency and the psychosemantics of most. Natural Language Semantics, 19(3), 227–256.

Marušič, F., Plesničar, V., Razboršek, T., Sullivan, J., & Barner, D. (2016). Does grammatical structure accelerate number word learning? Evidence from learners of dual and non-dual dialects of Slovenian. PloS one, 11(8).

Tools for thinking: 3D icons for embodied / enactive argumentation

Menno van Calcar & Floris Velema, Erasmus University Rotterdam

There are many tools (linguistic, formal, physical, social) which we manipulate to constitute and augment our cognitive abilities. In mathematics such tools are abundantly used, and philosophers and cognitive scientists try to understand how our embodied and enactive manipulations of pen and paper, rulers, fingers, apps to visualize equations and manipulate shapes, etc form or transform our mathematical abilities. Tools that can be used for the manipulation of arguments, however, are quite rare, as far as we know. Dealing with arguments is commonly seen as a typical representation-hungry cognitive activity, which resists interpretation along the lines of E-cognition. We disagree with this common conception, arguing that the formal structure of argumentation can be bodily manipulated, and that this manipulation then becomes part and parcel of the ability to deal with arguments.

Philosophicons (www.philosophicons.com) offers a way to represent the formal structure of arguments in a 3D-design. Philosophicons give implications, propositions, modes of reasoning etc distinct physical icons, thus allowing the 3D-representation of formal structure, regardless of semantical content. Working from an embodied/enactive perspective, we suspect that visualizing the logical structure and physically manipulating these icons partly constitutes the ability to deal with – the properties of – arguments. Several sets have been printed and are tested in secondary education.

Since this project is work in progress, we can only give a coarse-grained analysis and aim at presenting our ideas and findings so far, hoping for a lot of feedback.

SKILL

Daan Dronkers, Erasmus University Rotterdam

Mathematical knowledge is practical knowledge: more than mathematical facts, it involves mathematical skills — e.g. the skill to solve equations. Taking inspiration from Wittgenstein, I will talk about an understanding of skill according to which skill is the possibility for intentional action. I will first explain why intentional action should be understood in a way roughly equivalent to Anscombe’s 1957 account. I then explain that we must understand the modal dimension skill gives to intentional action as a form of extrapolation: to say that a student has the skill to solve equations is to extrapolate intentional equation solving to different contexts. Private language considerations introduce a practice of equation solving to rigidify the action across contexts. Practical knowledge, then, is knowledge of practice.

An embodied instrumentation case study in trigonometry

Rosa Alberto, Utrecht University

There is increasing attention for the embodied and extended nature of mathematical cognition but the bodies of literature on embodied and on extended cognition have developed mostly separately. We have conducted design research from these two theoretical perspectives to promote their integration and guide the development of digital design to foster mathematical learning in trigonometry. The frameworks embodied design and instrumental genesis inspired us to elicit the phenomenon embodied instrumentation: learning via techno-physical interaction with digital artifacts. A case study illustrates the design features of the digital artifact and the subsequent problem solving by a student (aged 16), who uses her body and the digital artifact to solve trigonometric equations in the unit circle and sine graph. We first reflect on the development of mathematical techno-physical coordinations in trigonometry and then think ahead about the decomposition of trigonometric coordinations in sequenced tasks and the embedding of techno-physical learning with digital artifact in real-life mathematical classrooms.

About the Mathematics that is Done to Us

Jean-Francois Maheux, UQAM

Some say that mathematics is not so much something we do, as it is something that is done to us. Artist Carl Andre (2004) captured a similar tension: “Art is what we do; culture is what is done to us” (p. 23). We are familiar with the distinction between doing mathematics (when math is what we do) and learning about mathematics (when math is a set of ideas and procedures to understand, memorize, etc., imposed to us). In this presentation, I aim to explore this relationship, and shed some positive light on the notion of mathematics as something “done to us” by conceptualizing the situation dialectically: Mathematics as a practice implies both doing mathematics and mathematics being done to us. From that angle, the question concerns mathematical activity itself. When working on a problem, there is a part where we exert control, freely deciding what move we try, and navigate our way through. But we do this with concepts and rules established before us, that are then “imposed” (or “imposes themselves”) on our activity. More so, one can argue that every step we take while doing mathematics also “frames” our next (possible) move. We are thus simultaneously both active and passive subjects in relation with mathematics. In this talk, I offer to theoretically and empirically reflect on the idea of seeing the relationship between what we do and what is done to us mathematically as a driving force in the discipline, and in what it means to be “mathematically able”.

Andre C. (2004). Carl Andre. In Peggy Gale (Ed) Artists talks. Press of the NSCAD.

When does sensory-motor experience become mathematical? An activity theory perspective

Anna Shvarts, Utrecht University

Embodied approaches to learning state the importance of sensory-motor actions for mathematics learning. Following the understanding of knowledge as a possibility of sensory-motor action (Radford, 2013), we question the conditions when practicing these actions leads to mathematical knowledge. We present an activity theory account of this problem by analyzing the embodied actions within the general structure of activity (Leont’ev, 1978). To describe the structure of embodied operations within an object-oriented action, we use the notion of a functional system. Further, we stress that the teaching/learning process is inevitably social, even if no teacher is present. In the presentation, we will focus on a case of one student who was practicing embodied action-based design (Abrahamson, 2014) for a sine function alone, without a tutor or interviewer. We analyze the communication between a student and a researcher that occasionally occurred as the researcher was steering the student towards an independent practice. Given the predisposed knowledge of participating in a study of mathematics learning, the student tended to reflect on his sensory-motor coordination spontaneously.  However, the researcher did not support this reflection and required to continue the sensory-motor practice itself. In a while, the student appropriated this pure motor task and practiced the performance thoroughly. In the following trigonometry problem-solving stage he did not actualize elaborated sensory-motor coordination. This analysis reveals the need to consider the prospectively mathematical sensory-motor actions within the broader structure of socially established teaching/learning activity that determines the “whole task” (Newman, Griffin, & Cole, 1989), which is broader than a particular motor task. An activity theory approach suggests that any knowledge is crystallized labor (Radford, 2013), which is a transformative activity. Thus the embodied actions are crystallized into mathematical knowledge in case a student enacted them within an activity that was directed to mathematical or mathematics teaching/learning achievements. However, the limits of embodied experience transfer between different activities are still under the question.